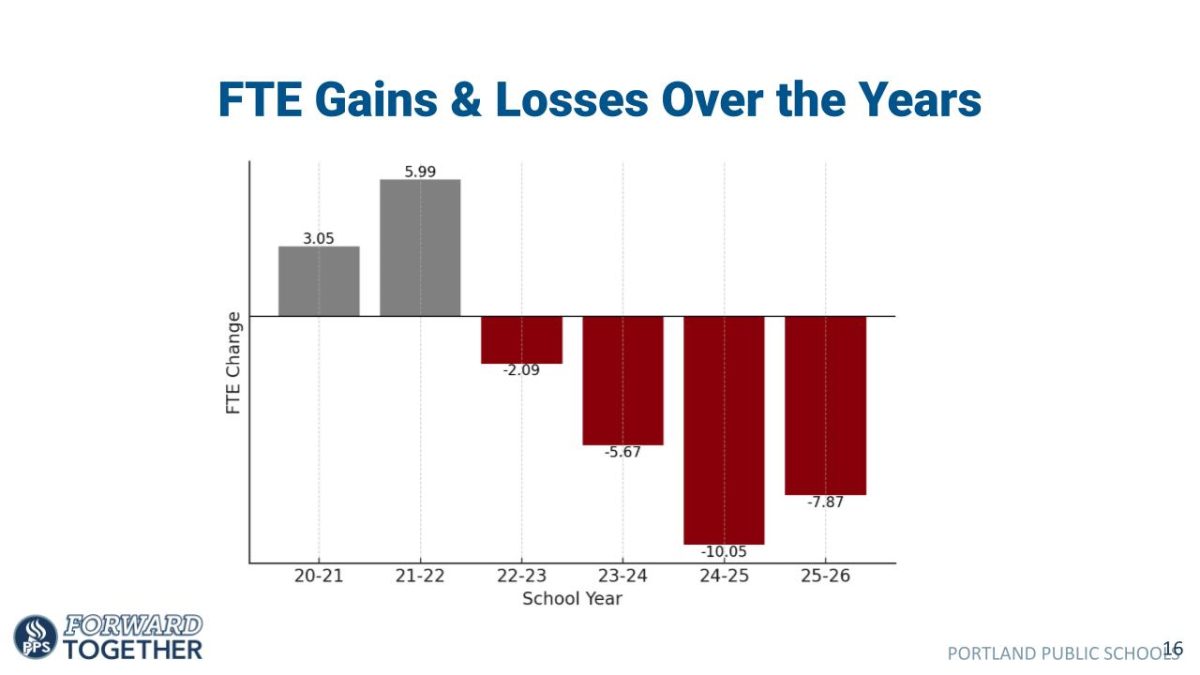
What can we really know? The question initially seems impossible to answer, given just how much stuff there is to know. It’s almost easier to answer what we can’t know. Even though there are still a lot of things we don’t yet know, most of them will have attainable answers eventually. For the most part, the only things we can’t know are the things beyond the physical; we can’t truly know what happens after death until we experience it, and if nothing happens, we will never know. There are things we can never observe. But from an epistemological standpoint (epistemology is the branch of philosophy pertaining to knowledge), the question poses a challenge for a different reason; as it turns out, it’s very difficult to truly know anything.
To accurately answer what we can know, we first need to understand how we can know. There are really only two ways we can learn. The first is through deductive reasoning, which is math, or formal logic; starting with a set of rules, and following them out to a logical conclusion. Deductive reasoning has no room for interpretation. As long as its premises are true, and you reasoned it correctly, the conclusion must be true. In theory, this means that deduction can be used to prove things, and can therefore be a means of gaining knowledge (in theory; we’ll get to that in a bit).
The second type of reasoning is induction. Inductive reasoning is observing a pattern and expanding it outwards to assume that the pattern works the same everywhere else. For example, science is inherently inductive. Experimentation is a form of induction, as is any kind of data analysis that makes inferences based on the patterns in the data. Most science is observing how things seem to work and creating models to represent them, an inductive process. However, due to the nature of induction, while it can be used as pretty strong evidence towards something being true, it can never be used as proof of anything; both because interpretations of the observations can vary, and because outside of exactly the sample you tested, the results could be completely different. Consider the following scenario: Today is your birthday. Yesterday, you were X-1 years old. Today, you are X years old. Using induction, you could then make the assumption that tomorrow, you will be X+1 years old. The reasoning is valid, but the conclusion is wrong; it comes from an understanding of what’s happening, but not why it’s happening, so it doesn’t take into account the way we count years. Any number of other conclusions could be inductively made, though. Maybe age increments randomly, or alternates between incrementing after a day and decrementing after a month. You could also come to the correct conclusion about the way that age increments, but you wouldn’t have a way of knowing it.
The deductive approach to the same problem would involve already knowing how we count age. If you already know that numerical age is counted in years, rounded to the previous whole number, then on your birthday, you can accurately deduce that in one year your age will be X+1.
So, how is this at all relevant? If this instance of induction led to invalid conclusions, then not all induction is correct (an example of deduction). But then, how do we know that any induction is valid? Well, because it’s worked in the past.
But there’s a problem with that. “Because it’s worked in the past” is inductive, and therefore cannot be proven. This is the problem of induction, first proposed by the 18th century philosopher David Hume, which argues that there is no non-circular way to justify induction. Deduction also can’t be used to justify it, because deduction can only conclude certainties, and, as established, the reliability of induction is already uncertain.
Induction can’t be used to truly know anything. But where does that leave us? All that’s left to know is what little can be deduced—except there’s a problem with that, too. To make any deduction work, agreements need to be made about the rules that it uses. These rules must either be reasoned (the flaws in which have already been demonstrated), or postulated. Postulates are, in essence, the things that we agree upon without justification so that everything can work. For example, the most fundamental rules of math and logic are postulates; if A implies B, and B implies C, then A implies C. It’s very intuitive, and it would be hard to imagine it working differently, but it also doesn’t come from any reasoning. The problem is, postulates are inherently unjustified. Not only that, but they can and have been challenged to great effect. The Greek mathematician Euclid, often referred to as the father of geometry, proposed a set of postulates that, for over a millennium, served as the basis for essentially all planar geometry. But in the last couple of centuries, Non-Euclidean geometry—that is, geometry that intentionally breaks Euclid’s postulates—has found an important use. It becomes necessary when doing math on two-dimensional planes that have been curved throughout three-dimensional space, or three-dimensional spaces curved in four-dimensional space (more or less how Einstein got to relativistic physics). The thing is, even if you challenge postulates, you still need postulates to support the challenge; and ultimately, it’s postulates all the way down. Because of this, deduction is also ineffective as a way to gain knowledge.
We can probably never truly know anything. Does that matter? If we can’t know anything, why not live your life as though the only things that are true are those that are most convenient to you, or adopt a philosophy such as solipsism, the idea that you are the only being to actually exist? There’s actually a really simple argument against solipsism, and it has nothing to do with whether or not to believe it. If you spend your life treating other people as though they don’t exist, and you’re wrong, the moral repercussions are a lot worse than if you spend your life treating people as though they do exist, and end up being wrong. While solipsism isn’t realistically a conclusion that you would come to from the inability to know, I bring it up because the argument is really similar. Although we can’t know, we still need induction and deduction. Without them, we couldn’t function; we would have no way of knowing that each day would look roughly the same as the last, and we could never make decisions except by completely arbitrary means. It would be impossible and nonsensical to fully renounce all reasoning, and it’s not what we should be aiming for anyway. If you were to try, it would more likely end up being a justification for renouncing only the reasoning that you dislike; just recognizing all of the reasoning that you already use would be pretty much impossible, so it would be an argument irrationally weighted in your favor. Like in the argument against solipsism, while it might lead to the best life for you, if you’re wrong, the moral repercussions branch out beyond you.
There’s one final point that needs to be addressed here, and that is the distinction between knowledge and understanding. To know something is definitive: that thing is exactly as I know it to be and works exactly as I know it to work. Understanding can be more fluid. It can be the culmination of observation, and represent ambiguity, and evolve with time as information and situations change. When I gave science as an example of induction, it was not to say that our inability to achieve true knowledge renders it worthless; if anything, the opposite. Science has never claimed to know, only sought to understand. In the absence of knowledge, understanding is the most valuable thing that we have.